动态规划
动态规划特点
- 计数
- 有多少种方式走到右下角
- 有多少种方式选出k个数使得和是sum
- 求最大最小值
- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度
- 求存在性
- 取石子游戏,先手是否必胜
- 能不能选出k个数使得和是sum
动态规划组成部分
- 确定状态
- 最后一步(最优策略种使用的最后一枚硬币ak)
- 化为子问题(最少的策略拼出最小的的面值27-ak)
- 转移方程
- f[X]=min{f[X-2]+1,f[X-5]+1,f[X-7]+1}
- 初始化条件和边界情况
- f[0]=0,如果不能拼出Y,f[Y]=正无穷
- 计算顺序
- f[0],f[1],f[2]…
- 消除冗余,加速计算
动态规划实例
求最大最小值动态规划
- 你有三种硬币,分别面值2元,5元和7元,每种硬币都有足够多
- 买一本书需要27元
- 如何用最少的硬币组合正好付清,不需要对方找钱
动态规划组成部分一:确定状态
确定状态需要两个意识:
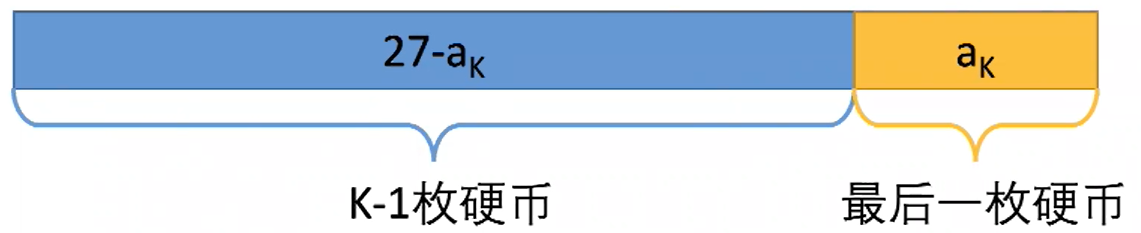
- 最后一步
- 关键点1:我们不关心前面的k-1枚硬币是怎么拼出27-ak的,而且我们现在甚至不知道ak和k,但是我们可以确定前面的硬币拼出了27-ak
- 关键点2:因为是最优策略,所以拼出27-ak的硬币数一定要最少,否则就不是最优策略
- 子问题
- 所以我们要求:最少用多少枚硬币可以拼出27-ak
- 原问题是最少用多少枚硬币拼出27
- 我们将原问题转化成一个子问题,而且规模最小:27-ak
- 为了简化定义,我们设定状态f(X)=最少用多少枚硬币拼出X
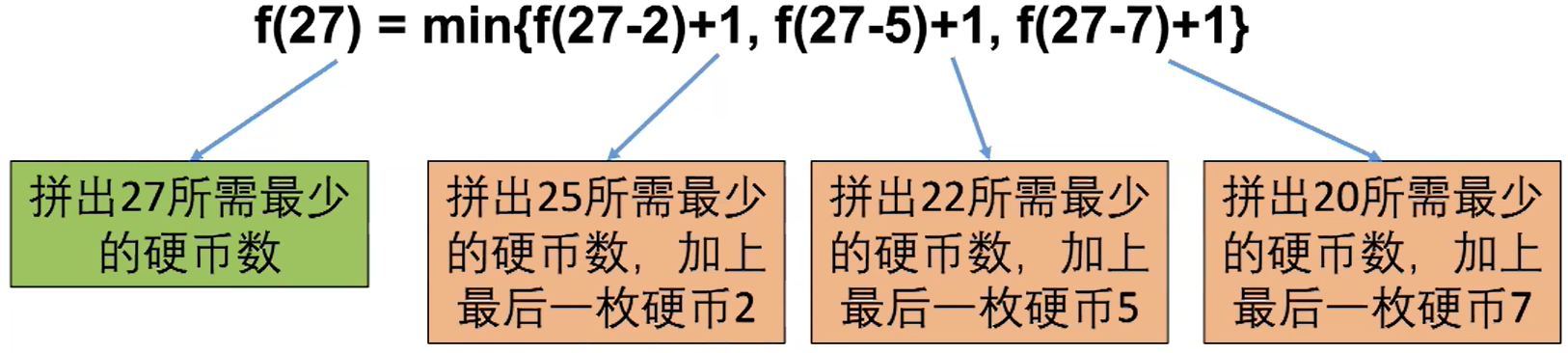
- 最后一枚硬币只可能是2,5或者7
- f(27)=min{f(27-2)+1,f(27-5)+1,f(27-7)+1}
动态规划组成部分二:转移方程
- 设状态f[X]=最少用多少枚硬币拼出X
- 对于任意X,f[X]=min{f[X-2]+1,f{X-5}+1,f[X-7]+1}
动态规划组成部分三:初始条件和边界情况
f[X]=min{f[X-2]+1,f[X-5]+1,f[X-7]+1}
两个问题:X-2,X-5或者X-7小于0怎么办?什么时候停下来?
如果不能拼出Y,就定义f[Y]=正无穷
所以f[1]=min{f[-1]+1,f[-4]+1,f[-6]+1}=正无穷,表示拼出来1
初始条件:f[0]=0 (用转移方程算不出来,需要手工定义)
动态规划组成部分四:计算顺序
- 拼出X所需要的最少硬币数:f[X]=min{f[X-2]+1,f[X-5]+1,f[X-7]+1}
- 初始条件:f[0]=0
- 然后计算f[1],f[2]……f[27]
- 当我们计算到f[X]时,f[X-2],f[X-5],f[X-7]都已经得到结果了

结论
- 每一步尝试三种硬币,一共27步
- 与递归算法相比,没有任何重复计算
- 算法时间复杂度(即需要进行的步数):27*3,大于递归时间复杂度:>> 27*3
// num表示硬币有哪些面值,n表示num数组的大小,cost表示总共需要多少钱
int pingyingbi(int *num,int n,int cost)
{
int f[cost+1];
int i=0;
int j=0;
f[0]=0;
// 求出当前操作系统int能取的正数最大值
int MAXNUM=(~((int)0))&(~(1<<(sizeof(int)*8-1)));
for(i=1;i<=cost;i++){
f[i]=MAXNUM;
for(j=0;j<n;j++){
if(i-num[j]>=0&&f[i-num[j]]<=MAXNUM-1){
if(f[i]>f[i-num[j]]+1){
f[i]=f[i-num[j]]+1;
}
}
}
}
if(f[cost]==MAXNUM){
return -1;
}
return f[cost];
}计数型动态规划
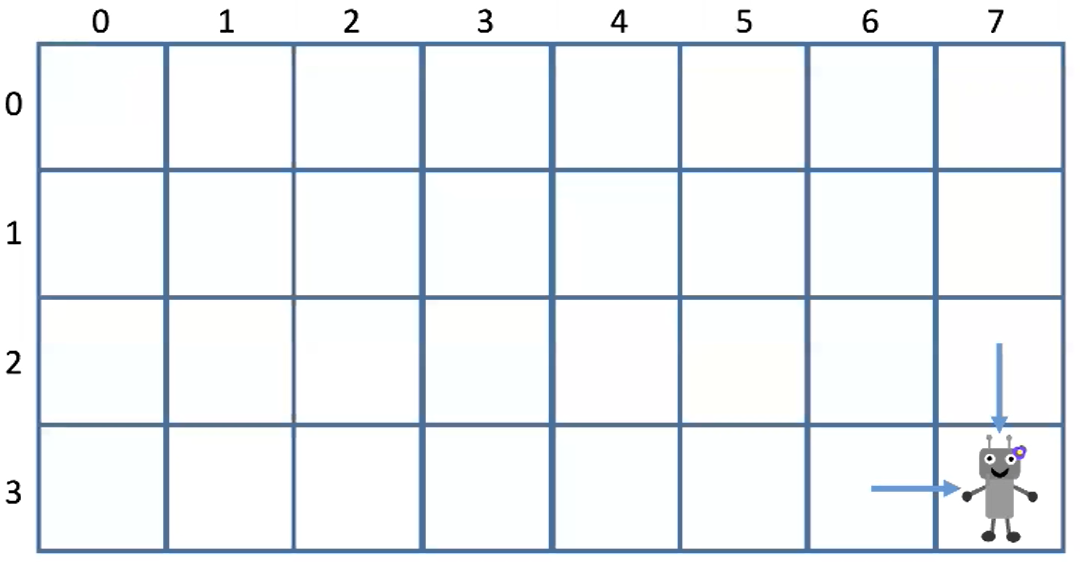
- 给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者向右走一步
- 问有多少种不同的方式走到右下角
动态规划组成部分一:确定状态
- 最后一步:无论机器人用何种方式到达右下角,总有最后挪动的一一步:向右或者向下
- 右下角坐标设为(m-1,n-1)
- 那么前一步机器人一定是在(m-2,n-1)或者(m-1,n-2)
动态规划组成部分一:子问题
- 那么,如果机器人有X种方式从左上角走到(m-2,n-1),有Y种方式从左上角走到(m-1,n-2),则机器人有X+Y种方式走到(m-1,n-1)
- 问题转化为,机器人有多少种方式从左上角走到(m-2,n-1)和(m-1,n-2)
- 原题要求有多少种方式从左上角走到(m-1,n-1)
- 转化为规模更小的子问题
- 状态:设f[i][j]为机器人有多少种方式从左上角走到(i,j)
动态规划组成部分二:转移方程
对于任意一个格子(i,j),都有f[i][j]=f[i-1][j]+f[i][j-1]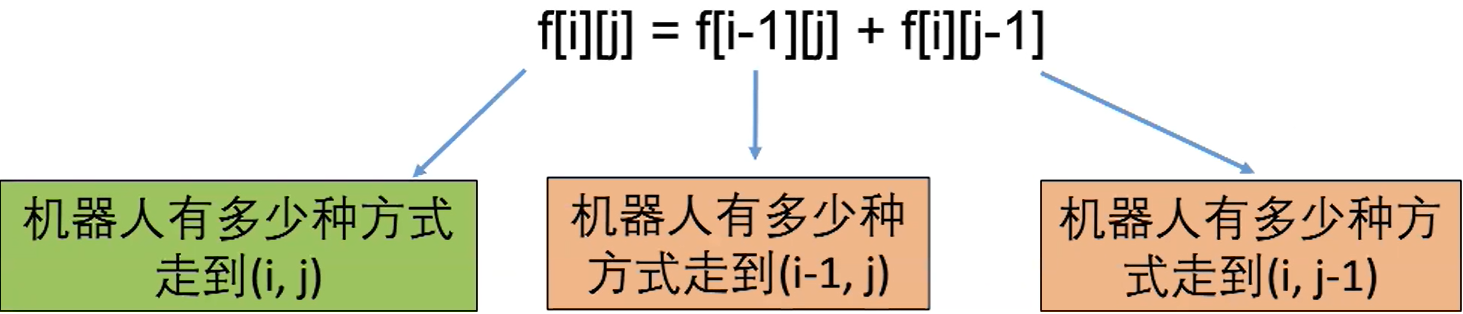
动态规划组成部分三:初始条件和边界情况
- 初始条件:f[0][0]=1,因为机器人只有一种方式到左上角
- 边界情况:i=1或j=0,则前一步只能有一个方向过来f[i][j]=1
动态规划组成部分四:计算顺序
- f[0][0]=1
- 计算第0行:f[0][0],f[0][1],…,f[0][n-1]
- …
- 计算第m-1行:f[m-1][0],…..,f[m-1][n-1]
- 时间复杂度(计算步数):O(MN),空间复杂度(数组大小):O(MN)
int findwaynum(int m,int n)
{
int map[m][n];
int i=0;
int j=0;
for(i=0;i<m;i++){
for(j=0;j<n;j++){
if(j==0||i==0){
map[i][j]=1;
}else{
map[i][j]=map[i-1][j]+map[i][j-1];
}
}
}
return map[m-1][n-1];
}存在型动态规划
- 有n块石头分别在x轴的0,1,…,n-1位置
- 一只青蛙在石头0,想跳到石头n-1
- 如果青蛙在第i块石头上,它最多可以向右跳距离ai
- 问青蛙能否跳到石头n-1
- 例子:输入:a=[2,3,1,1,4],输出:true;输入:a=[3,2,1,0,4],输出:false
动态规划组成部分一:确定状态
- 最后一步:如果青蛙能跳到最后一块石头n-1,我们考虑它跳的最后一步
- 这一步是从石头i跳过来,i<n-1
- 这需要满足两个条件:青蛙可以跳到石头i;最后一步不超过条约的最大距离:n-1-i<=ai
动态规划组成部分一:子问题
- 那么,我们需要知道青蛙能不能跳到石头i(i<n-1)
- 而我们原来要求青蛙能不能跳到石头n-1
- 变成一个规模更小的子问题了,状态:设f[j]表示青蛙能不能跳到石头j
动态规划组成部分二:转移方程
- 设f[j]表示青蛙能不能跳到石头j
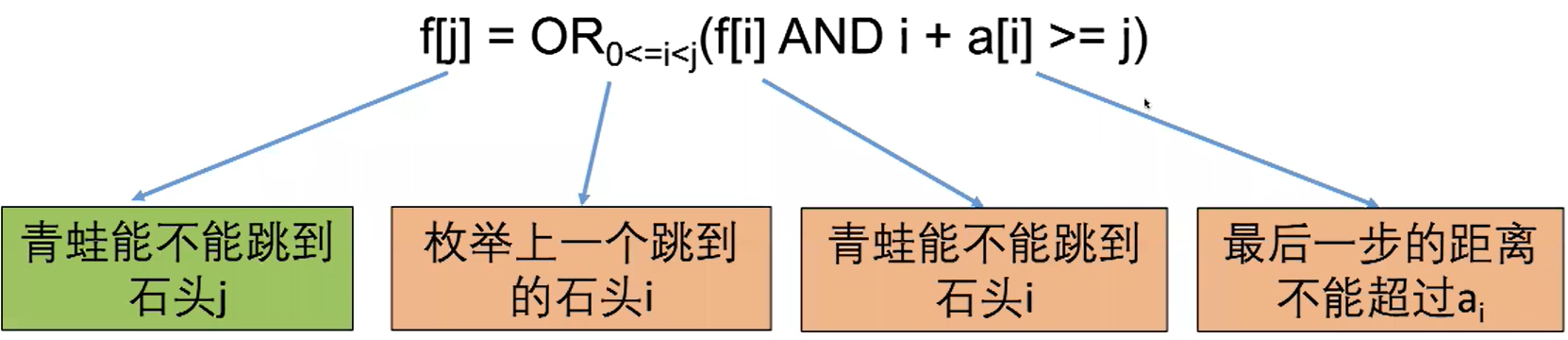
动态规划组成部分三:初始条件和边界情况
- 设f[j]表示青蛙能不能跳到石头j
- 初始条件:f[0]=true,因为青蛙一开始就在石头0
动态规划组成部分四:计算顺序
- 设f[j]表示青蛙能不能跳到石头j
- f[j]=OR0<=i<j(f[i] AND i+a[i]>=j)
- 初始化f[0]=true
- 计算f[1],f[2],…,f[n-1]
- 答案是f[n-1]
- 时间复杂度:O(N2),空间复杂度(数组大小):O(N)
#define true 1
#define false 0
int qingwatiao(int *num,int n)
{
int pd[n];
int i;
int j;
pd[0]=true;
for(i=1;i<n;i++){
pd[i]=false;
for(j=0;j<i;j++){
if(pd[j]==true&&i-j<=num[j]){
pd[i]=true;
break;
}
}
}
return pd[n-1];
}// 问题:给定一个整形数组,求该数组中,连续的子序列的乘积达到最大,该数组可以包含负数和0;例如[2,4,5,-1,3,0],则输出20
// 该函数原理动态规划
// i的值始终大于等于j,于是pd[i][j]表示num[j]*num[j+1]* ... *num[i]
// 所以pd[i][j]=num[j]*num[j+1]* ... *num[i]=pd[i][j+1]*num[j]
// 初始条件当i=j时,pd[i][j]=num[i]=num[j]
#include <stdio.h>
int maxmuti(int *num,int n)
{
// 当前max为当前操作系统下int最小的负数
int max=(int)1<<(sizeof(int)*8-1);
int pd[n][n];
int i=0;
int j=0;
for(i=0;i<n;i++){
for(j=i;j>=0;j--){
if(i==j){
// 假设i和j的值相同时,是本身,也就是当传进来数组为[500,-2,1]时,该函数会返回500
// 传进来的是[500]时,该函数会放回500
pd[i][j]=num[i];
if(pd[i][j]>max){
max=pd[i][j];
}
}else{
pd[i][j]=pd[i][j+1]*num[j];
if(pd[i][j]>max){
max=pd[i][j];
}
}
}
}
return max;
}
int main()
{
int num[]={41,0,10,-1,5,6};
printf("%d\n",maxmuti(num,sizeof(num)/sizeof(int)));
return 0;
}


